This post continues where part 1 ended. In order to increase the accuracy of our function solver we are going to use a 4th order Runga Kutta algorithm. The basics are the same as with the Euler method. However the dy part of the 4th order method is more accurately computed.
Definition
The incremental values of this method are defined as:
With the factors k1 - k4 being:
The function f is again the derivative of y.
Code
Lets see how this looks in Python.
def runga_kutta_4(t, f, initial=(0, 0)):
"""
Runga Kutta nummerical method.
Computes dy and adds it to previous y-value.
:param t: (list/ array) Time values of function f.
:param f: (function)
:param initial:(tpl) Initial values
:return: (list/ array) y values.
"""
# step size
h = t[1] - t[0]
y = np.zeros((t.size, ))
t[0], y[0] = initial
for i in range(t.size - 1):
k1 = h * f(t[i], y[i])
k2 = h * f(t[i] + h * 0.5, y[i] + 0.5 * k1)
k3 = h * f(t[i] + h * 0.5, y[i] + 0.5 * k2)
k4 = h * f(t[i + 1], y[i] + k3)
y[i + 1] = y[i] + (k1 + 2 * k2 + 2 * k3 + k4) / 6
return y
As you can see above the input values are the same as with euler function. Again the starting point of the curve must be set by passing the initial values for t0 and y0.
By plotting all 3 curves, the Euler method, the 4th order Runga Kutta method and the function y = et than we find that the curve of the Runga Kutta method is plotted above the curve of the solution and thus has far more acccuracy than the Euler method.
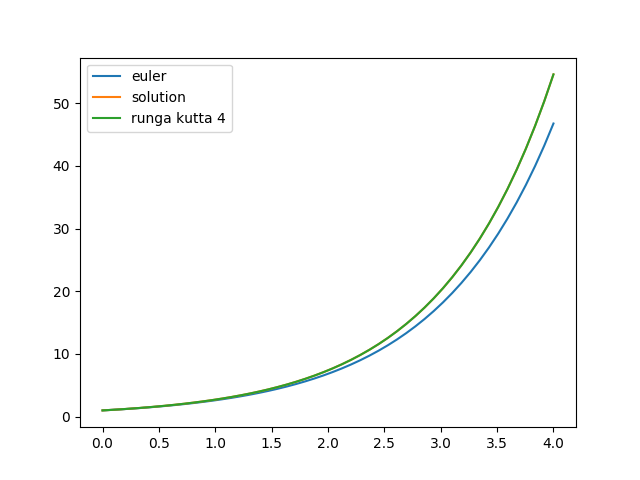
Euler method, Runga Kutta method and solution.
In the next post we are going to apply the Runga Kutta solution to the vibrations problem.